Definitions for Synthetic Seismograms
Synthetic
seismograms are computed by assuming a mathematical model with a particular
geometry of the source and velocity layering that approximates an elastic
or anelastic earth.Solutions of
varying approximations to the wave equation in the geometry of the model
result in theoretical amplitude versus time of arrival times or wavefield
seismograms.These may be used for
studying wave propagation through various media, calculating amplitude
and waveform responses to various sources in different models and for comparison
with observed seismograms to infer the model.The
calculation of synthetic seismograms normally requires a solution to the
wave equation for the geometry and characteristic parameters of the model.This
entails application of appropriate boundary conditions exactly or numerically.
(1) Models
Many are either 1, 2, or 3-dimensional as shown in Figure 1
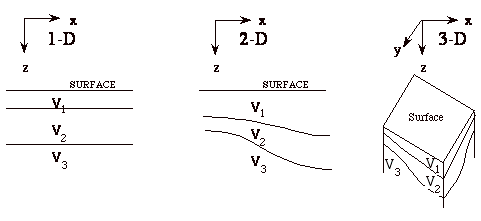
Figure
1--1, 2 and 3D Models
(2) Elastic
Parameters (a,b,r)
| 1-D | 2-D | 3-D |
|---|---|---|
(3) Seismograms,
displacement u, w, v in x1, x2, x3 in Cartesian
coordinates.
| 1-D | 2-D | 3-D |
|---|---|---|
| u(x1,t) | u(x1,x2,t) | u(x1,x2,x3,t) |
| w(x1,t) | w(x1,x2,t) | w(x1,x2,x3,t) |
| v(x1,t) | v(x1,x2,t) | v(x1,x2,x3,t) |
(Note that a 1-D model will produce seismograms that are different for various distances (due to various angles of incidence).In exploration seismology, it is common to refer to a 1-D model and 1-D synthetic seismograms which are for vertical incident waves only.)
(4)
Propagation Types
| Acoustic | Elastic | Seismic (anelastic) |
|---|---|---|
| fluid, pressure wave only | solid, no absorption | solid, including absorption |
(5)
Wave Types
| Acoustic | Elastic | Seismic (anelastic) |
|---|---|---|
| P, SV, SH | P SV |
Love (SH), Rayleigh higher modes (equivalent to guided waves) |
(6)
Source (at surface or depth)
| Point Sources | Finite Sources |
|---|---|
| Vertical Force Explosive (compressional) Double Couple |
Fault Plane Summed vectors Summed Green's functions Source time history |
(7)
Wave-Theory or Ray-Theory
| Wave Approach | Ray Theory Approach |
|---|
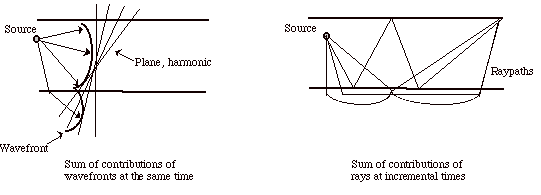
(8)
Anelasticity
Wave Theory - causal or acausal Q introduction by complex velocities
Ray Theory - causal Q operator (A (t, t*))
There is an extensive literature pertaining to various synthetic seismogram methods. However, much confusion on the terminology of various methods exists and only a few review-type papers are available Chapman, 1977; Helmberger and Burdick, 1979; Cerveny and Ravindra, 1971;and Cerveny et al., 1977, Lay and Wallace, 1996). For body-wave problems Chapman (1977) reviews various ray-theoretical and wave-theoretical synthetic seismogram methods for the case of 1-D models. He shows that in this case the basic equation consists of a double integral transformation
![]()
where
u is the seismogram of (vector) displacement, u(w,p,z)is
the frequency domain displacement response function (complex reflection
coefficients), and the exponential term represents a plane harmonic wave
with frequency, w, and slowness
p.The various synthetic seismogram
methods solve this integral equation using a variety of approaches which
are related by Table 1.In addition
a brief description of the various synthetic seismogram methods is given
in Table 2.
 Return to GG6220 home
Return to GG6220 home Return to lecture handouts
Return to lecture handouts
This page was last modified Mar 6, 2007.
Contact rbsmith@mines.utah.edu
with questions about this page.
URL of this page is
http://www.mines.utah.edu/~rbsmith/TEACHING/GG6220/SynthSeis.html