Theoretical Seismology
Spring Semester, 2005
Due: April 19, 2005
Homework #3--Earthquake Source Theory
1. Do problem 3.4 in Aki and Richards.
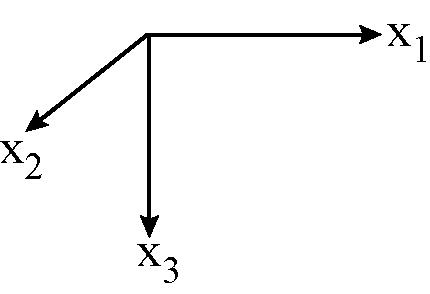
2. Use the coordinate system where
is along strike, 
is in the direction of increasing depth, and
is
perpendicular to the 
plane. For point sources:
a) What are the equivalent forces for a pure strike-slip earthquake on the plane
= 0?
b) What are the equivalent forces for pure dip-slip faulting on
the plane = 0?
c) What are the equivalent forces for pure tension on the plane
= 0?
d) Suppose the fault plane makes an angle
such
that =
tan
.
If we consider the
plane as the Earth's free surface, this would correspond to the plane with a dip
angle of 90° - .
What are the equivalent forces for a pure strike-slip earthquake on this fault
plane?
e) What are equivalent forces for a pure dip-slip earthquake on the fault plane of part (d)?
f) Suppose on the plane = 0, one has a uniformly constant velocity, v, moving dislocation x1,
and a is the final length of the fault. With the slip components on the fault of si:
s1 = H(vt - x1 {H(x1) - H(x1 - a)};
and s2 = s3 = 0.
What are the equivalent forces?
3. With reference to Figure 3.6, p. 48, of Aki and Richards, vol. 1, the authors state that this force system is equivalent to the force system shown in Figure 3.5.
a) Is it true that the two force systems are equivalent? Justify your answer by explicitly stating the conditions under which equivalence holds.
b) If the two force systems are equivalent, are both valid descriptions of an earthquake which is thought to be the result of slip on a plane? Again, justify your answer. Consider all of our assumptions in deriving the equivalent force representation.
4. For the following fault plane orientations; determine: a) the moment tensor, Mo b) the eigenvalues (Mo) and eigenvectors of each tensor, and 3) draw a lower-hemisphere fault plane solution representing for each focal mechanism including the locations of the P-, T- and B-axes. This can be done with either some Fortran codes or a new mac code that I will give you.
| Fault Type | Fault Strike () |
Dip ( ) |
Slip ( ) |
|---|---|---|---|
| a) Vertical strike-slip | 0° | 90° | 0° |
| b) 45° dip-slip | 0° | 45° | 90° |
| c) Vertical dip-slip | 0° | 90° | 90° |
5. Moment Tensor Interpretation--As an example of moment tensor inversion, consider the moment tensor of a real earthquake, the Miyagi-Oki earthquake of June 12, 1978, which was an intermediate-depth earthquake in the Kurile Islands subduction zone near Japan. The moment tensor inverted was
| 0.1178 | ±0.1692 | ±0.0626 | ||
| M | = | ±0.1692 | ±1.5433 | ±1.4358 |
| ±0.0626 | ±1.4358 | ±1.4255 |
in units of 1027 dyne-cm.
For the problem:
a) Diagonalize the moment tensor into its appropriate isotropic, major double-couple and minor double-couple components. Explain why there may be erratic solutions for the components.
b) Then zero out the isotropic component and determine its major double-couple and minor double-couple components.
c) What percentage of the source is minor vs. major double-couple?
d) Determine the directions of the P-, T- and B-axes for the major double-couple source.
e) Using these axes and your knowledge of the tectonics of this region, determine what type of earthquake it represents and the strike and dip of the fault. What are strike and dip of the auxiliary plane?
f) Plot out on a focal sphere the proper orientation of these planes and the P-, T-, and B-axes.
Return to GG6220 home
Return to problem sets
This page was last modified Mar 6 2007.
Contact
rbsmith@mines.utah.edu with questions about this page.
URL of this page is
http://www.mines.utah.edu/~rbsmith/TEACHING/GG6220/PROBLEMS/Prob3.momenttensor.html