(Modal surface wave and finite difference and finite element methods not included)
Basic equation for a synthetic seismogram u(t, x1, x2)
![]()
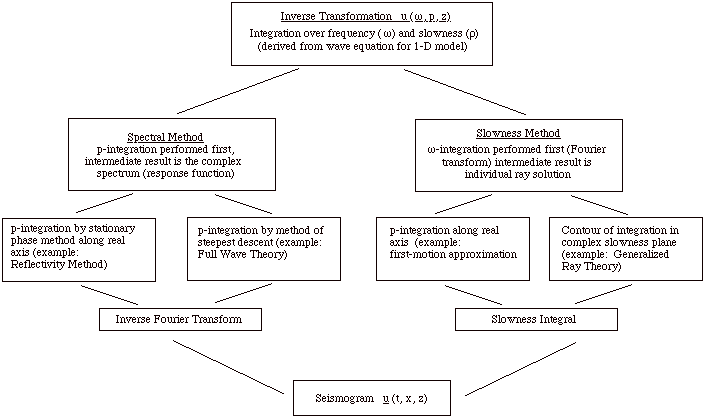
Flow Chart for calculating seismograms starting from the frequency domain formulation of a seismogram u (w,p,z)
SUMMARY OF SYNTHETIC SEISMOGRAM METHODS
|
Method |
Brief Description |
Geometrical Considerations |
Computational Considerations |
Key References |
||
|
1. Geometrical Ray Theory (Geometrical Optics) GO |
Travel-times, reflection coefficients, geometrical spreading effects by geometrical optics. Corresponds to high frequency (WKBJ) approximation. Often called 'Ray Theory'. Zero-order (first term of ART expression). |
Plane (or spherical) homogeneous layers or velocity gradients easily included. Any geometry possible (but cumbersome) by Snell's law ray tracing. |
Fast calculation. Inaccurate near critical points and for head waves due to WKBJ approximation which assumes smooth (wrt l) velocity variation, valid when D(p) slowly varying. |
Bullen, 1963; Cerveny and Ravindra, 1971; Gerver and Markushevich, 1967. |
||
|
2. Asymptotic Ray Theory ART
|
Represents the solution to the wave equation as a series expansion of individual rays. As many terms as necessary for accuracy can be used. If only the first term is used, ART becomes the GO solution under the WKBJ approximation. |
Same as GO. Solutions valid if sufficient terms are used and the phase function (wavefronts) t(x,y,z) is analytic. |
Requires choice of cut-off of infinite series expansion. |
Cerveny and Ravindra, 1971, Chap. 2; Karal and Keller, 1959. |
||
|
3. Generalized Ray Theory (Exact Ray Theory) GRT
Cagniard - de Hoop
|
Expansion of full wave response in terms of a large number of rays (ray types) with each ray given by a series expansion (ART) sufficient to accurately predict the wave response. Total response is the sum of the responses for individual rays. Velocity is made proportional to depth in each layer so that no true head waves are included. |
1-D Models only. Velocity function approximated by many thin layers. |
Body wave response only. Capable in including complex source functions. Requires Q information by Q operator. |
Gilbert and Helmberger, 1972; Helmberger, 1968; Wiggins and Helmberger, 1974; Wiggins and Madrid, 1974; Chapman, 1967, 1974, 1976; Helmberger and Harkrider, 1978. |
||
|
4. Disk Ray Theory (Quantized Ray Theory, QRT; first Motion Approximation, FMA) DRT |
Energy assumed to propagate as rays which are traced through velocity model, but the contribution of each ray is added to each seismogram by projecting the arrival time along the travel-time curve, thus approximating a wavefront. |
Extremely simple to use for 1-D velocity models. Can be used for 2-D models as long as
ray-tracing can be performed. |
Fast calculation compared to Reflectivity, GRT and finite difference. Can include 1-D or 2-D models. Single-frequency Q can be included. |
Wiggins and Madrid, 1974; Wiggins, 1976; Chapman, 1976; McMechan, 1974. |
||
|
5. Reflectivity Method RM |
Response of 1-D model to spherical point source represented by sum of plane wave responses at various frequencies. Integration of Thomson-Haskell Reflectivity matrix terms over angle of incidence and then fourier transform to obtain seismogram. |
1-D model, source and receivers at surface. Q may be introduced using complex velocities. |
Computational effort increases rapidly with number of layers, frequency of source, phase velocity range of interest. |
Fuchs and Mueller, 1971; Braile and Smith, 1975; Braile, 1977; Mueller and Kind, 1976. |
||
|
6. Modified Reflectivity Method MRM |
Integration over wavenumber using Harkrider's formulation of the Thomson-Haskell matrix including various source types. Numerical integration over the wavenumber and then Fourier Transformation. Source is vertical point force, explosive point source, or double couple. |
1-D model, source at depth, receivers at surface. P-SV, Rayleigh motion included. Depth phases such as pP included because of proper treatment of free surface in the reflectivity zone. |
Anelasticity included by complex velocities, calculation over a range of phase velocities. Costs increase with frequency, number of layers and phase velocity range. |
Kind, 1978; Harkrider, 1964.
|
||
|
|
7. Propagator Matrix Response PMR |
The propagator matrix response of layered half space is used in the reflectivity calculations instead of the Thomson-Haskell matrices. |
Same as MM |
Same as MM |
Gilbert and Backus, 1966; Kennett, 1974, 1979, 1980; Kennett and Kerry, 1979; Kennett et al, 1978; Woodhouse, 1978; Hudson, 1969. |
|
|
|
8. Full Wave Theory FWT |
Extension of the reflectivity or propagator matrix methods which allow accurate computation near turning points in layers with velocity gradients resulting in interference head waves. |
Same as MRM except gradients in layers. |
Same as MRM |
Cormier and Richards, 1977; Choy, 1977. |
|
|
|
9. Normal Mode Summation NMS |
Utilize the dispersion relations and amplitude functions (eigenvalues) for Rayleigh or Love (SH) motion to determine the amplitude and phase spectrum for a layered half space at a given distance. Fourier transformation then yields the synthetic surface wave seismograms. A large number of modes can be included. Body wave arrivals can be calculated if sufficiently high mode number is used. |
1-D model. Source at depth. |
Must sum a large number of modes to approximate broadband data and body waves. Numerical effects due to high mode number and long period require large number of layers in model which can increase computational effort significantly. |
Kerry, 1981; Kennett and Kerry, 1979; Buland and Gilbert, 1980; Knopoff, Schwab and Kausel, 1973. |
|
|
|
10. Finite Difference FD |
Finite Difference expressions for spatial and temporal derivatives of the wave equation for elastic media for propagation of displacements, velocity or stresses are solved directly. Solutions for a grid of displacement and velocity points are determined at each time and then propagated from the initial conditions to an arbitrary number of time steps. |
1, 2 or 3-D models can be utilized although 2-D is most useful and computationally feasible. Sources and receivers located arbitrarily in model. Free surface and absorbing boundaries at edges of the model must be included. Point or earthquake sources can be included. |
Grid spacing (10 points per wavelength) and time step (small step to insure stability) requirements result in very large computer time and storage use. Explicit schemes are slow, may be unstable, but are accurate. Implicit schemes are more complicated, may be inaccurate, but are much faster and insure stability. |
Boore, 1970, 1972; Mazzella, 1979; Espindola, 1979; Bouchon, 1980; Claerbout, 1978; Alterman and Karal, 1968; Madariaga, 1976; Alford et al., 1974; Kelley et al., 1975. |
|
|
|
11. Finite Element FE |
Direct numerical solution of wave equation by FE matrix methods. In concept, similar to FD, but matrix inversions required by FE methods. |
Same as FD |
Large (banded) matrices must be inverted. |
Smith, 1974, 1975; Lysmer and Drake, 1972. |
|
 Return to GG6220 home
Return to GG6220 home Return to lecture handouts
Return to lecture handouts
This page was last modified Mar 6 2007.
Contact
rbsmith@mines.utah.edu with questions about this page.
URL of this page is
http://www.mines.utah.edu/~rbsmith/TEACHING/GG6220/IntroWaveTheory.htm